Dundas Chart for SharePoint Send comments on this topic.
Correlation Formula
See Also

Glossary Item Box

Overview

This formula shows the strength of the relationship that exists between two random variables.

Applying the Formula

All statistical formulas are calculated using the Statistics class, and the following table describes how to use the Correlation method.

 

Value/Description Example
Formula Name: Correlation Statistics.Correlation ("Series1", "Series2")
Parameters:
  1. firstInputSeriesName: The name of the Series object that stores the first group's data.
  2. secondInputSeriesName: The name of the Series object that stores the second group's data. An exception will be raised if the input series do not have the same number of data points.
Statistics.Correlation("Series1", "Series2")
Return: A double that represents the correlation value between the two groups of data.

 

 

Note
Make sure that all data points have their XValue property set, and that their series' XValueIndexed property has been set to false.
Statistical Interpretation

The correlation value is always between -1 and 1, and if X and Y are completely independent their correlation is zero. If the correlation coefficient is positive then when X is large, Y will also be large, and they are then said to be positively correlated. The more closely related X and Y are, the closer the correlation coefficient is to 1. On the other hand, if the correlation is negative, then Y is more likely to be small when X is big. They are then negatively correlated, and the negative relationship is stronger the closer the correlation coefficient is to 1.

 

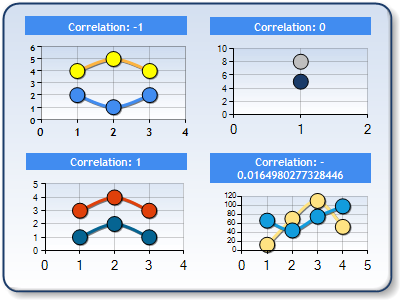Figure 1: Four chart areas, composed of two data series each; chartarea1 (top-left) is negatively correlated, chartarea2 (bottom-left) is positively correlated, chartarea3 (top-right) has a no correlation, and chartarea4 (bottom-right) has a negative correlation of 0.0164,

 

The definition of the correlation coefficient is the following:

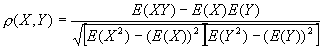
Example

This example demonstrates how to get the correlation coefficient between two groups of data (Series1 and Series2). and return the result as a double.

Visual Basic Copy Code
' Get the correlation.
Dim result As Double = chartObj.DataManipulator.Statistics.Correlation("Series1", "Series2")
C# Copy Code
// Get the correlation.
double result = chartObj.DataManipulator.Statistics.Correlation("Series1", "Series2");

See Also

Formulas
Formulas Overview

Statistical Formulas
Using Statistical Formulas