Overview
This formula measures the degree of dependence that may exist between two random variables.
Applying the Formula
All statistical formulas are calculated using the Statistics class, and the following table describes how to use its Covariance method to get the covariance.
| Value/Description | Example | |
|---|---|---|
| Formula Name: | Covariance | Statistics.Covariance("Series1", "Series2") |
| Parameters: | Statistics.Covariance("Series1", "Series2") | |
| Return: | A double that represents the covariance value between the two groups of data. |
- |
 Note Note |
|---|
| Make sure that all data points have their XValue property set, and that their series' XValueIndexed property has been set to false. |
Statistical Interpretation
Suppose X and Y are two random variables. If X and Y are very closely related, learning the value of X tells you much about the value of Y. If they are only slightly related, then knowing the value of X helps a little, but not much, when trying to guess the value of Y.
The quantity that measures the degree of dependence between two random variables is called covariance, and the covariance of X and Y is defined as follows:
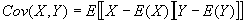
Suppose that when X is larger than E(X), you know that Y is also larger than E(Y). In that case, will be positive. In general, when two random variables tend to move together, their covariance is positive. And if two random variables tend to move in the opposite direction (for example, if X tends to be big at the same time Y is small, and vice versa) then their covariance is negative.
The following is a short-cut formula that is much easier to use than the defining formula:
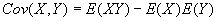
Cov(X,Y) is equal to zero if X and Y are independent. If Cov(X,Y) is nonzero, then we know that X and Y are not independent .
Example
This example demonstrates how to get the covariance between two groups of data (Series1 and Series2), and then return the covariance between the two groups as a double.
| Visual Basic |  Copy Code Copy Code |
|---|---|
| |
| C# |  Copy Code Copy Code |
|---|---|
| |
Formulas
Formulas Overview
Statistical Formulas
Using Statistical Formulas





