Overview
Perform a T Test using Students distribution (T distribution) with unequal variances.
Applying the Formula
All statistical formulas are calculated using the Statistics class, and the following table describes how to use its TTestUnEqualVariances method to perform the test.
|
Value/Description |
Example |
| Formula Name: |
T Test with Unequal Variances |
Statistics.TTestUnEqualVariances(0.2, 0.05, "Series1", "Series2"). |
| Parameters: |
- hypothesizedMeanDifference: the hypothesized difference between the means of the data groups.
- probability: the alpha value (probability).
- firstInputSeriesName: The name of the Series object that stores the first group of data.
- secondInputSeriesName: The name of the Series object that stores the second group of data
|
Statistics.TTestUnEqualVariances(0.2, 0.05, "Series1", "Series2") |
| Return: |
A TTestResult object, which has the following members:
- FirstSeriesMean
- SecondSeriesMean
- FirstSeriesVariance
- SecondSeriesVariance
- TValue
- DegreeOfFreedom
- ProbabilityTOneTail
- TCriticalValueOneTail
- ProbabilityTTwoTail
- TCriticalValueTwoTail
|
- |
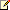 Note Note |
| Make sure that all data points have their XValue property set, and that their series' XValueIndexed property has been set to false. |
Statistical Interpretation
Suppose that you have two different populations whose means you want to compare. Assume that the random variables  (mean
(mean  , variance
, variance  ) and
) and  (mean
(mean  , variance
, variance  ) have approximately normal distributions. For sample sizes of
) have approximately normal distributions. For sample sizes of  and
and  , then the sample means
, then the sample means  and
and  are normal random variables.
are normal random variables.
If we want to test hypotheses about the difference between the population means  , our null hypothesis might be that the population means are equal:
, our null hypothesis might be that the population means are equal:
 or
or  .
.
If the population variances  and
and  are unknown, we will have to use T statistics (if variances are known we use Z Statistics). If the null hypothesis is true, and if we also know that
are unknown, we will have to use T statistics (if variances are known we use Z Statistics). If the null hypothesis is true, and if we also know that  then
then  has a t distribution where
has a t distribution where  .
.
Calculation
- Calculate
 and
and  .
.
- Calculate the sample variances (with n-1 in the denominator) for both samples:
 and
and  .
.
- Calculate the pooled estimator
 :
:  .
.
- Calculate the test statistic T:
 .
.
- If the null hypothesis is true, then T will have a t distribution.
Example
This example demonstrates how to perform a t test with unequal variances for two groups of data represented by Series1 and Series2. The results are returned in an TTestResult object. The object values are then added as titles to a separate chart. We assume series data was added at design-time. Further, we assume a "DundasBlue" template was applied for appearance purposes.
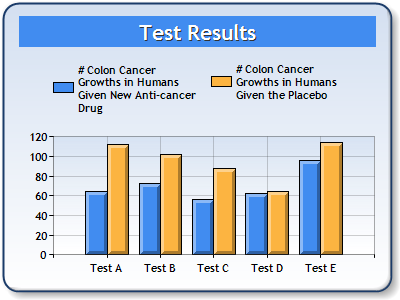  |
| Figure 1: Two Charts; One containing Series data (left), and the other containing the TTestResult object (right). |
| Visual Basic |
 Copy Code Copy Code |
' Perform the test.
ttestresult = chartObj.DataManipulator.Statistics.TTestUnEqualVariances(0.2, 0.05,
"Series1", "Series2")
' Add Title to second chart.
chart2.Titles.Add("TTestResult Object")
chart2.Titles.Add("Hypothesized Mean Difference: 0.2 | Probability: 5%")
' Change Appearance properties of first title.
chart2.Titles(0).BackColor = Color.FromArgb(255, 65, 140, 240)
chart2.Titles(0).Font = New Font("Trebuchet", 12, FontStyle.Bold)
chart2.Titles(0).Color = Color.White
chart2.Titles(0).Style = TextStyle.Shadow
' Change Appearance properties of second title.
chart2.Titles(1).BackColor = Color.FromArgb(255, 224, 64, 10)
chart2.Titles(1).Font = New Font("Trebuchet", 8, FontStyle.Bold)
chart2.Titles(1).Color = Color.White
chart2.Titles.Add("Degree Of Freedom: " + ttestresult.DegreeOfFreedom.ToString())
chart2.Titles.Add("First Series Mean: " + ttestresult.FirstSeriesMean.ToString() +
" | Second Series Mean: " + ttestresult.SecondSeriesMean.ToString())
chart2.Titles.Add("First Series Variance: " + ttestresult.FirstSeriesVariance.ToString() +
" | Second Series Variance: " + ttestresult.SecondSeriesVariance.ToString())
chart2.Titles.Add("Probability T One Tail: " + ttestresult.ProbabilityTOneTail.ToString())
chart2.Titles.Add("Probability T Two Tail: " + ttestresult.ProbabilityTTwoTail.ToString())
chart2.Titles.Add("T Critical Value One Tail: " + ttestresult.TCriticalValueOneTail.ToString())
chart2.Titles.Add("T Critical Value Two Tail: " + ttestresult.TCriticalValueTwoTail.ToString())
chart2.Titles.Add("TValue: " + ttestresult.TValue.ToString())
|
| C# |
 Copy Code Copy Code |
// Perform the test.
ttestresult = chartObj.DataManipulator.Statistics.TTestUnEqualVariances(0.2, 0.05,
"Series1", "Series2");
// Add Title to second chart.
chart2.Titles.Add("TTestResult Object");
chart2.Titles.Add("Hypothesized Mean Difference: 0.2 | Probability: 5%");
// Change Appearance properties of first title.
chart2.Titles[0].BackColor = Color.FromArgb(255, 65, 140, 240);
chart2.Titles[0].Font = new Font("Trebuchet", 12, FontStyle.Bold);
chart2.Titles[0].Color = Color.White;
chart2.Titles[0].Style = TextStyle.Shadow;
// Change Appearance properties of second title.
chart2.Titles[1].BackColor = Color.FromArgb(255, 224, 64, 10);
chart2.Titles[1].Font = new Font("Trebuchet", 8, FontStyle.Bold);
chart2.Titles[1].Color = Color.White;
chart11.Titles[1].Style = TextStyle.Shadow;
chart2.Titles.Add("Degree Of Freedom: " + ttestresult.DegreeOfFreedom.ToString());
chart2.Titles.Add("First Series Mean: " + ttestresult.FirstSeriesMean.ToString() +
" | Second Series Mean: " + ttestresult.SecondSeriesMean.ToString());
chart2.Titles.Add("First Series Variance: " + ttestresult.FirstSeriesVariance.ToString() +
" | Second Series Variance: " + ttestresult.SecondSeriesVariance.ToString());
chart2.Titles.Add("Probability T One Tail: " + ttestresult.ProbabilityTOneTail.ToString());
chart2.Titles.Add("Probability T Two Tail: " + ttestresult.ProbabilityTTwoTail.ToString());
chart2.Titles.Add("T Critical Value One Tail: " + ttestresult.TCriticalValueOneTail.ToString());
chart2.Titles.Add("T Critical Value Two Tail: " + ttestresult.TCriticalValueTwoTail.ToString());
chart2.Titles.Add("TValue: " + ttestresult.TValue.ToString());
|
 See Also
See Also
 Note
Note (mean
(mean  , variance
, variance  ) and
) and  (mean
(mean  , variance
, variance  ) have approximately normal distributions. For sample sizes of
) have approximately normal distributions. For sample sizes of  and
and  , then the sample means
, then the sample means  and
and  are normal random variables.
are normal random variables. , our null hypothesis might be that the population means are equal:
, our null hypothesis might be that the population means are equal: or
or  .
. and
and  are unknown, we will have to use T statistics (if variances are known we use Z Statistics). If the null hypothesis is true, and if we also know that
are unknown, we will have to use T statistics (if variances are known we use Z Statistics). If the null hypothesis is true, and if we also know that  then
then  has a t distribution where
has a t distribution where  .
. and
and  .
.
 and
and  .
.
 :
:  .
.
 .
.


 Copy Code
Copy Code Copy Code
Copy Code




