Use transformations to alter graphics operations by scaling, moving or rotating them. Multiple transformations can be applied to graphics. This section describes the possible transformation types, and how to combine them to achieve the effects you need. It covers the following topics:
Below is a list of the transformations supported by PDF Graphics .NET:
In the example below, a circle is painted onto the page. A translation is then applied, and the same circle painted again;
the second circle appears to the right of, and slightly below, the first.

After applying a scaling transformation, all subsequent graphics are scaled by the specified ratio along the axes. Use the TranslateScale method to perform the scaling operation. In the following example, a rectangle is drawn, and then a transformation is applied that scales graphics to half their size. The rectangle is then drawn again.
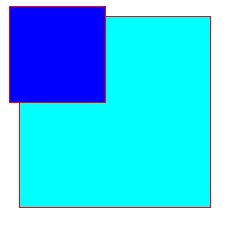
Note that the smaller rectangle is also positioned slightly to the left and above the larger one; it is painted at coordinate (10,10), which is scaled down to (5,5). Scaling affects not only the size of painted graphics but also their position.
Rotation of graphics is performed relative to the top-left corner of the page, in counter-clockwise fashion. The TranslateRotate method performs a rotation transformation, with the angle specified in radians, counter-clockwise. In the example below, text is drawn at various angles.

To ensure that the rotated text fits on the page, it is first translated 100 points towards the center of the page. This is an example of combining transformations, which will be covered later in this section.
Skewing can be seen as pulling on one side of the graphics coordinate space; either pulling the right-hand side up, or pulling the bottom side towards the left. The result is that the coordinate space appears lifted up on one side, or falling over to another. It is best explained through an example. See the code below:
A green rectangle is painted onto the page. Then, the coordinate space is skewed along the X axis. The result can be seen in the second picture, where the X axis of the dark rectangle is no longer horizontal; it's being pulled up. In the third picture, the Y axis is skewed. The rectangle appears to fall over to one side.

This example also shows how to save and restore the current graphics state; more on that further down. For a full explanation of graphics state preservation, see Graphics state.
All of the above transformations (translation, scaling, rotation and skewing) are essentially the same; they alter the current coordinate space matrix of the graphics target (page or stencil). Matrices have traditionally been used to represent common graphics transformations. If required, a free-form transformation can be performed by supplying a suitable matrix to the Transform method. For more information, see the Matrix class reference documentation.
Coverage of graphics transformations through matrices is beyond the scope of this section, but numerous examples can be found on-line. The Adobe PDF specification also includes an explanation of graphics coordinate transformation.
Transformations can be combined. When combining, the order of transformations is important; scaling followed by a rotation is different from a rotation followed by scaling. Take the following example:
This creates two pages. On the first page, the green rectangle is moved 100 points down and to the right, and then rotated. On the second page the coordinate space is rotated first, and then moved down and to the right.
Coordinate transformations remain in effect after drawing operations. To reset the coordinate system, use the BeginContainer and EndContainer methods. These methods store the current state of the transformation matrix and restore a previous state, respectively.
Storing and restoring state is not limited to a single level; numerous states can be stacked with successive calls to BeginContainer. Each EndContainer call restores the previous state until the coordinate space has been reset to its initial values.
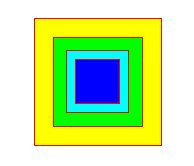
In the following example, a number of squares is painted onto the page, using a transformation for each. The transformations are then restored, and the rectangles outlined: