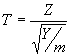Overview

Returns the t-value of the Student's t-distribution as a function of probability and degrees of freedom.

Applying the Formula

All statistical formulas are calculated using the Statistics class, and the following table describes how to use its  InverseTDistribution method.

Statistical Interpretation

Another important distribution that is related to the normal distribution is the t distribution. Suppose that Z and Y are independent random variables. Let Z be a standard normal random variable (mean of 0, variance of 1). And Y a chi-square variable with m degrees of freedom. Let us make the definition:

Then it is said that the variable T has the t distribution with m degrees of freedom (The t distribution is sometimes called Students distribution).

Looking at the form of the density function provides some clues about the nature of the t distribution. Since g(x) = g(-x), it follows that the density function is symmetric about x = 0. The maximum value of g(x) occurs when x = 0.

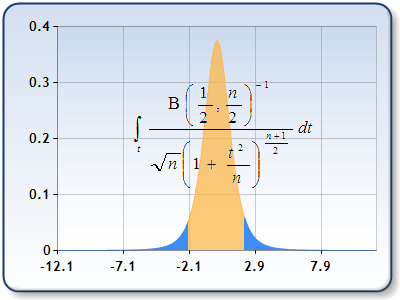
Figure 1: T distribution.

The density function has a bell shape that is roughly similar to the standard normal distribution. A t random variable has a higher chance of being far from 0 than does a standard normal random variable. However, as the number of degrees of freedom increases the t distribution approaches very close to the standard normal distribution.

Example

This example demonstrates how to calculate the Inverse T distribution probability.

Visual Basic	Copy Code
Imports Dundas.Charting.WebControl ... ' Calculate Inverse T distribution probability. double result = Chart1.DataManipulator.Statistics.InverseTDistribution(.05, 15)

C#	Copy Code
using Dundas.Charting.WebControl; ... // Calculate Inverse T distribution probability. double result = Chart1.DataManipulator.Statistics.InverseTDistribution(.05, 15);

See Also