Note
Make sure that all data points have their XValue property set, and that their series'  XValueIndexed property has been set to false.

Statistical Interpretation

The correlation value is always between -1 and 1, and if X and Y are completely independent their correlation is zero. If the correlation coefficient is positive then when X is large, Y will also be large, and they are then said to be positively correlated. The more closely related X and Y are, the closer the correlation coefficient is to 1. On the other hand, if the correlation is negative, then Y is more likely to be small when X is big. They are then negatively correlated, and the negative relationship is stronger the closer the correlation coefficient is to -1.

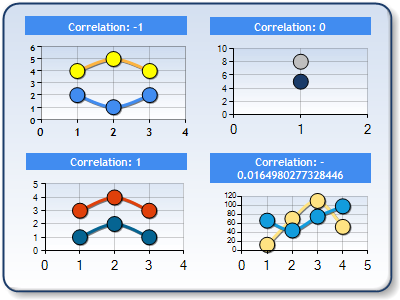Figure 1: Four chart areas composed, of two data series each;  chartarea1 (top-left) is negatively correlated,  chartarea2 (bottom-left) is positively correlated, chartarea3 (top-right) has a no correlation, and chartarea4 (bottom-right) has a negative correlation of 0.0164,

The definition of the correlation coefficient is the following:

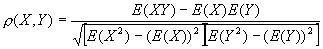
Example

This example demonstrates how to get the correlation coefficient between two groups of data (Series1 and Series2). and return the result as a double.

Visual Basic	Copy Code
Imports Dundas.Charting.WinControl ... ' Get the correlation. Dim result As Double = Chart1.DataManipulator.Statistics.Correlation("Series1", "Series2")

C#	Copy Code
using Dundas.Charting.WinControl; ... // Get the correlation. double result = Chart1.DataManipulator.Statistics.Correlation("Series1", "Series2");